
Computational Science is the research field devoted to the study of mathematical models, numerical methods and computational algorithms to understand and solve complex problems arising in applied sciences and engineering. With the aim of bringing theoretical developments and real-world applications together, Computational Science combines several disciplines such as numerical analysis, mathematical modeling and software implementation.
The research activities of the group include model order reduction of parametrized problems, numerical methods for partial differential equations, optimization and feedback control, uncertainty quantification, data assimilation and machine learning.
Many modern mathematical models of real-life processes pose challenges when used in numerical simulations, due to complexity and large size (dimension). Model order reduction aims to lower the computational complexity of such problems by reducing the model’s associated state space dimension or by reducing number of parameters by choosing only important ones. Computational science group works with implementation of reduced basis methods and with computing related a-priori and a-posteriori error estimation.
REDUCED BASIS METHODS
OPTIMAL CONTROL AND DATA ASSIMILATION
Optimization and control theory deals with finding a control for a dynamical system over a period of time such that a cost function is minimized/maximized. In the computational science group, we deal with optimal control, multi objective optimisation combined with reduced basis techniques and data assimilation. Most interesting example of optimal control system can be that if the dynamical system is a spacecraft, then we would want to control the rocket thrusters with the objective to reach the moon with minimum fuel expenditure.
STRUCTURE-PRESERVING NUMERICAL METHODS
COMPUTATIONAL PLASMA PHYSICS
DIMENSION
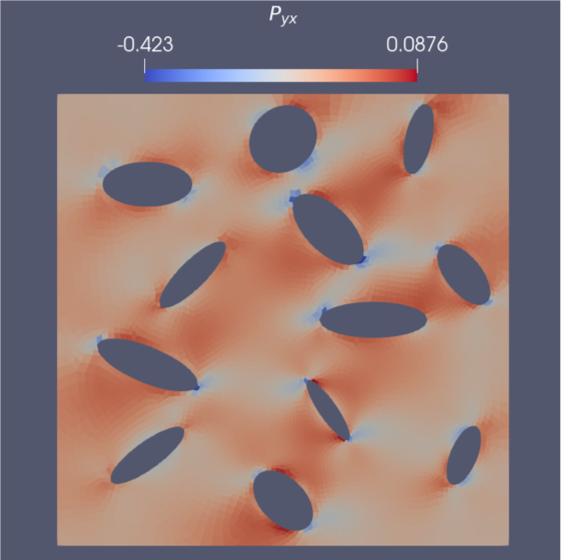
With the recent advances in additive manufacturing, there has been a growing interest in designing microstructures with optimal macroscopic properties for specific applications. To study these structure-property relations, two-scale problems, in which the macro- and microstructures are simultaneously modelled and coupled, are typically solved. However, solving such problems is computationally expensive and infeasible in multi-query contexts such as material design and optimization, where numerous forward solutions are required.
NON-LINEAR TWO-SCALE (META-) MATERIAL DESIGN
In this project, different model order reduction techniques for the acceleration of the microscopic problem are explored, considering non-linearities in the geometry and material behavior. Moreover, consistent sensitivities for material design are also derived.
REDUCED ORDER MODELING FOR (VARIATIONAL) DATA ASSIMILATION
This project focuses on the integration of reduced order modeling (ROM) techniques in a data assimilation framework. Of primary interest is the inverse problem of estimating states and parameters relying on real-time and historical experimental data. We look at the problem both from a deterministic perspective, developing 3D/4D-VAR based methods, and from a stochastic perspective, studying new implementations of the ensemble Kalman filter (EnKF) and other ensemble based methods. Overall, we pay special attention on the treatment of the representation error introduced by the use of approximate and incomplete models. In parallel, we investigate the development of better experimental set-ups by employing optimal experimental design techniques. These too are supported by the use of reduced order modeling techniques, in particular of reduced basis methods.
The goal of this project is to solve an inverse problem in the context of single-scale and two-scale thermal, mechanical and coupled multiphysics problems. The focus of the project is on applications in computational material science – phenomena such as piezoelectric response, sintering and curing processes. One of the most relevant inverse problems deals with estimation of microstructural properties given macroscale measurement data. Solving inverse problems of this type requires several forward solves which are computationally expensive. In order to accelerate estimation of material properties and other parameters we develop (non-intrusive) reduced order models which are also efficient in dealing with non-linearities. In addition we develop offline-efficient dimensionality reduction techniques, which possess a better generalization accuracy and are physically consistent, for settings where full-order snapshots are limited or expensive. This is achieved by combining ingredients from the field of model order reduction and scientific machine learning. Currently, we use these developed techniques to solve aforementioned practical inverse problems.
ACCELERATING INVERSE ESTIMATION IN COMPUTATIONAL MATERIAL SCIENCE
OPTIMAL EXPERIMENTAL DESIGN IN THE PRESENCE OF THE MODEL BIAS
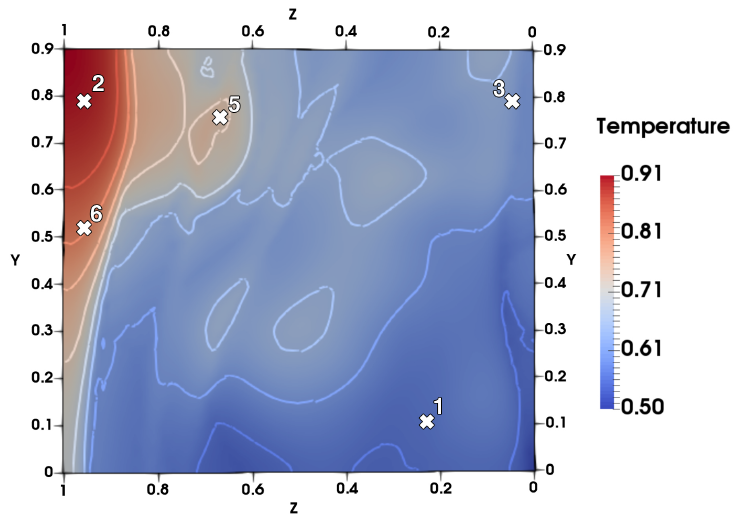
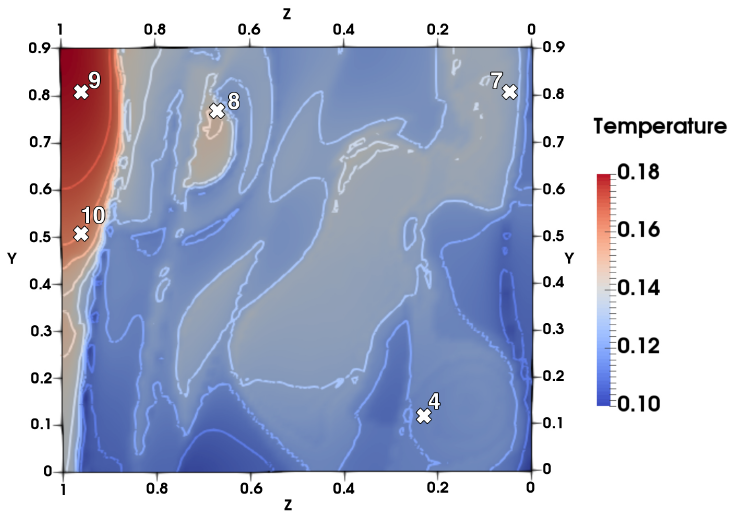
Mathematical models often depend on parameters, such as source terms or material properties. The values of these parameters are known with some uncertainty. Measurement data can be used to reduce this uncertainty and thereby improve the model’s credibility.
The first question of this project concerns the choice of the measurements or the experiments that are the most informative. This question is particularly important in the sparse data setting when only a limited number of measurements are available due to their cost. The reduction in parameter uncertainty improves the model’s credibility only under the assumption of the perfect model. In reality, a model is an imperfect and biased approximation of a real-world process. For that reason, in order to further improve the model’s credibility one needs to take into account the model bias. This corresponds to the second main question that this project tackles.
These questions lie in the field of optimal experimental design (OED). The main objective of the project is to develop OED methods for the selection of experiments for problems with linear and non-linear parameter dependence. To this end, we are taking a Bayesian point of view and developing a numerical framework that combines physics-based models with measurement data in order to improve the model credibility under the assumptions of model imperfection or bias, and the measurement noise. Furthermore, by integrating our OED approach with a surrogate model we aim to develop the framework which is fast and scalable with respect to the different experimental configurations.
Faculty
Postdocs
PhD students
- Calculus variant 2 (2WBB0) – Bachelor College Basic course – co-lecturers:
2022
Journal Publications:
- J. S. Hesthaven, C. Pagliantini, and N. Ripamonti, Adaptive symplectic model order reduction of parametric particle-based Vlasov-Poisson equation, 2022, (Submitted) In: arXiv. 2201.05555.
- C. Pagliantini, and F. Vismara, Gradient-preserving hyper-reduction of nonlinear dynamical systems via discrete empirical interpolation, Jun 2022, (Submitted) In: arXiv. 2206.01792.
- J. S. Hesthaven, C. Pagliantini, and N. Ripamonti, Rank-adaptive structure-preserving model order reduction of Hamiltonian systems, 8 Mar 2022, In: ESAIM : Mathematical Modelling and Numerical Analysis. 56, 2, p. 617-650 34 p.
- J. S. Hesthaven, C. Pagliantini, and G. Rozza, Reduced basis methods for time-dependent problems, 2022, In: Acta Numerica. 31, p. 265-345
2021
Journal Publications:
- C. Pagliantini, Dynamical reduced basis methods for Hamiltonian systems, Jun 2021, In: Numerische Mathematik. 148, 2, p. 409–448 40 p.
- C. Pagliantini, G. Manzini, O. Koshkarov, G. L. Delzanno, and V. Roytershteyn, Energy-conserving explicit and implicit time integration methods for the multi-dimensional Hermite-DG discretization of the Vlasov-Maxwell equations, 21 Oct 2021, (Submitted) In: arXiv.
- J. S. Hesthaven, and C. Pagliantini, Structure-preserving reduced basis methods for Poisson systems, Jul 2021, In: Mathematics of Computation. 90, 330, p. 1701-1740 40 p.
- O. Koshkarov, G. Manzini, G. L. Delzanno, C. Pagliantini, and V. Roytershteyn, The multi-dimensional Hermite-discontinuous Galerkin method for the Vlasov-Maxwell equations, Jul 2021, In: Computer Physics Communications. 264, 35 p., 107866.
- M. H. Abbasi, S. Naderilordejani, C. Berg, L. Iapichino, W. H. A. Schilders, and N. van de Wouw, An Approximate Well-Balanced Upgrade of Godunov-Type Schemes for the Isothermal Euler Equations and the Drift Flux Model with Laminar Friction and Gravitation, Apr 2021, In: International Journal for Numerical Methods in Fluids. 93, 4, p. 1110-1142 33 p.
- S. Naderilordejani, B. Besselink, M. H. Abbasi, G. O. Kaasa, W. H. A. Schilders, and N. van de Wouw, Control-oriented modelling for managed pressure drilling automation using model order reduction, May 2021, In: IEEE Transactions on Control Systems Technology. 29, 3, p. 1161-1174 14 p., 9099213.
- X. Cao, P. Benner, I. Pontes Duff, and W. H. A. Schilders, Model order reduction for bilinear control systems with inhomogeneous initial conditions, 2021, In: International Journal of Control. 94, 10, p. 2886-2895 10 p.
- H. Bansal, P. Schulze, M. H. Abbasi, H. Zwart, L. Iapichino, W. H. A. Schilders, and N. van de Wouw, Port-Hamiltonian formulation of two-phase flow models, Mar 2021, In: Systems and Control Letters. 149, 9 p., 104881.
- D. Degen, K. Veroy, M. Scheck-Wenderoth, and F. Wellmann, Crustal-Scale Thermal Models: Revisiting the Influence of Deep Boundary Conditions, 14 Apr 2021, (Submitted) In: Earth and Space Science Open Archive.
- D. Degen, K. Veroy, J. Freymark, M. Scheck-Wenderoth, T. Poulet, and F. Wellmann, Global sensitivity analysis to optimize basin-scale conductive model calibration: A case study from the Upper Rhine Graben, Sep 2021, In: Geothermics. 95, 15 p., 102143.
- T. Guo, O. Rokoš, and K. Veroy, Learning constitutive models from microstructural simulations via a non-intrusive reduced basis method, 1 Oct 2021, In: Computer Methods in Applied Mechanics and Engineering. 384, 23 p., 113924.
- N. Vaidya, M. Baragona, V. Lavezzo, R. Maessen, and K. Veroy, Simulation study of the cooling effect of blood vessels and blood coagulation in hepatic radio-frequency ablation, 2 Feb 2021, In: International Journal of Hyperthermia. 38, 1, p. 95-104 10 p.
- T. Nolte, N. Vaidya, M. Baragona, A. Elevelt, V. Lavezzo, R. Maessen, V. Schulz, and K. Veroy, Study of flow effects on temperature-controlled radiofrequency ablation using phantom experiments and forward simulations, Sep 2021, In: Medical Physics. 48, 9, p. 4754-4768 15 p.
Conference Publications:
- J. S. Hesthaven, C. Pagliantini, and N. Ripamonti, Structure-preserving model order reduction of Hamiltonian systems, 25 Sep 2021, preprint.
- H. Bansal, S. Rave, L. Iapichino, W. H. A. Schilders, and N. van de Wouw, Model order reduction framework for problems with moving discontinuities, 2021, Numerical Mathematics and Advanced Applications, ENUMATH 2019 – European Conference: European Conference, Egmond aan Zee, The Netherlands, September 30 – October 4. Vermolen, F. J. & Vuik, C. (eds.). Cham: Springer, p. 83-91 9 p. (Lecture Notes in Computational Science and Engineering; vol. 139).
- H. Bansal, H. J. Zwart, L. Iapichino, W. H. A. Schilders, and N. van de Wouw, Port-Hamiltonian modelling of fluid dynamics models with variable cross-section, 1 Jun 2021, In: IFAC-PapersOnLine. 54, 9, p. 365-372 8 p.
- H. Bansal, S. Weiland, L. Iapichino, W. H. A. Schilders, and N. van de Wouw, Structure-Preserving Spatial Discretization of a Two-Fluid Model, 11 Jan 2021, 59th IEEE Conference on Decision and Control (CDC 2020). Institute of Electrical and Electronics Engineers, p. 5062-5067 6 p. 9304252. (Proceedings of the IEEE Conference on Decision and Control; vol. 2020-December).
- N. Aretz-Nellesen, P. Chen, M. Grepl, and K. Veroy, A Sequential Sensor Selection Strategy for Hyper-Parameterized Linear Bayesian Inverse Problems, 2021, Numerical Mathematics and Advanced Applications, ENUMATH 2019 – European Conference. Vermolen, F. J. & Vuik, C. (eds.). Cham, Switzerland: Springer, Vol. 139. p. 489-497 9 p.
2020
Journal Publications:
- M.H. Abbasi, L. Iapichino, B. Besselink, W.H.A. Schilders, N. van de Wouw, Error estimation in reduced basis method for systems with time-varying and nonlinear boundary conditions, Computer Methods in Applied Mechanics and Engineering (2020) 360, 112688.
- S. Naderi Lordejani, M.H. Abbasi, N. Velmurugan, C. Berg, J.A. Stakvik, B. Besselink, L. Iapichino, F. Di Meglio, W.H.A. Schilders, N. van de Wouw, Modelling and numerical implementation of managed pressure drilling systems for the assessment of pressure control systems, SPE Drilling & Completion (2020)
- M.H. Abbasi, S. Naderi Lordejani, C. Berg, L. Iapichino, W.H.A. Schilders, N. van de Wouw, A well-balanced Godunov-type Scheme for the isothermal Euler equations and the drift flux model with laminar friction and gravitation, International Journal for Numerical Methods in Fluids (2020)
- M.H. Abbasi, L. Iapichino, S. Naderi Lordejani, W.H.A. Schilders, N. van de Wouw, Reduced Basis Method for managed pressure drilling based on a model with local nonlinearities, International Journal for Numerical Methods in Engineering (2020)
- H. Bansal, P. Schulze, M.H. Abbasi, H. Zwart, L. Iapichino, W.H.A. Schilders, N. van de Wouw, Port-Hamiltonian formulation of two-phase flow models, Submitted to Systems & Control Letters (2020).
- X. Cao, P. Benner, I. Pontes Duff and W.H.A. Schilders, Model order reduction for bilinear control systems with inhomogeneous initial conditions, 18 Mar 2020, In : International Journal of Control.
Conference Publications:
- M. H. Abbasi, H. Bansal, H. Zwart, L. Iapichino, W. H. A. Schilders and N. van de Wouw, Power-preserving interconnection of single- and two-phase flow models for managed pressure drilling, 2020 American Control Conference (ACC), Denver, CO, USA, 2020, pp. 3097-3102, doi: 10.23919/ACC45564.2020.9147405.
- M.H. Abbasi, L. Iapichino, B. Besselink, W.H.A. Schilders, N. van de Wouw, Error estimates for model order reduction of Burgers’ equation, 2020, 21st IFAC World Congress.
- T.C.P.F. Leenen, S. Naderilordejani, B. Besselink, W.H.A. Schilders and N. van de Wouw. Control-oriented model reduction for a class of hyperbolic systems with application to managed pressure drilling, Jul 2020, (Accepted/In press) 21th IFAC world congress . 6 p.
2019
Journal Publications:
- M.H. Abbasi, S. Naderi Lordejani, N. Velmurugan, C. Berg, L. Iapichino, W.H.A. Schilders, N. van de Wouw, A Godunov-type scheme for the drift flux model with variable cross section, Journal of Petroleum Science and Engineering (2019) 179: 796-813.
- A. Di Buccanico, L. Iapichino, N. Litvak, F. Van der Meulen, R. Wehrens, Mathematics for Big Data, The Best Writing on Mathematics (2019), 120-131, Princeton University Press.
- P. Benner, X. Cao, and W.H.A Schilders. A bilinear H2 model order reduction approach to linear parameter-varying systems, 1 Dec 2019, In : Advances in Computational Mathematics. 45, 5-6, p. 2241–227131 p.
- G. De Luca, P. Bolcato, and W.H.A. Schilders. Proper initial solution to start periodic steady-state-based methods, 1 Mar 2019, In : IEEE Transactions on Circuits and Systems I: Regular Papers. 66, 3, p. 1104-1115 12 p., 8515269.
- N. Aretz-Nellesen, M. A. Grepl, and K. Veroy. 3D-VAR for parameterized partial differential equations: a certified reduced basis approach. Advances in Computational Mathematics 45, 2369-2400 (2019).
Conference Publications:
- X. Cao, J.M.L. Maubach, S. Weiland, and W.H.A. Schilders. A novel Krylov method for model order reduction of quadratic bilinear systems, 18 Jan 2019, 2018 IEEE Conference on Decision and Control, CDC 2018. Institute of Electrical and Electronics Engineers, p. 3217-3222 6 p. 8619575
2018
Journal Publications:
- R. Hiptmair, and C. Pagliantini, Splitting-based structure preserving discretizations for magnetohydrodynamics, SMAI Journal of Computational Mathematics, 4 (2018), pp. 225-257.
- B.A. de Dios, R. Hiptmair, and C. Pagliantini, Auxiliary space preconditioner for a DG discretization of H(curl;Omega)-elliptic problem on hexahedral meshes, Domain Decomposition Methods in Science and Engineering XXIV, Vol. 125. Lect. Notes Comput. Sci. Eng. Springer, Cham. (2018), pp. 223-231.
- G. Fabrini, L. Iapichino and S. Volkwein. Reduced-order greedy controllability of finite dimensional linear systems. IFAC-PapersOnLine, (2018) 51 (2), 296-301.
- A.K. Tyagi, X. Jonsson, T.G.F. Beelen, and W.H.A. Schilders, Hybrid importance sampling Monte Carlo approach for yield estimation in circuit design, 25 Oct 2018, In : Journal of Mathematics in Industry. 8, 1, 23 p., 8:11.
- S. Naderilordejani, B. Besselink, M.H. Abbasi, G.O. Kaasa, W.H.A. Schilders, and N. van de Wouw, Model order reduction for managed pressure drilling systems based on a model with local nonlinearities, 1 Jan 2018, In : IFAC-PapersOnLine. 51, 8, p. 50-55 6 p.
- S. Lungten, W.H.A. Schilders, and J.A. Scott, Preordering saddle-point systems for sparse LDLT factorization without pivoting, 1 Oct 2018, In : Numerical Linear Algebra with Applications. 25, 5, 13 p., e2173.
- S. Lungten, W.H.A. Schilders, and J.M.L. Maubach, Threshold incomplete factorization constraint preconditioners for saddle-point matrices, 15 May 2018, In : Linear Algebra and Its Applications. 545, May 2018, p. 76-107 32 p.
Conference Publications:
- A. Das, S. Weiland, L. Iapichino, Model approximation of thermo-fluidic diffusion processes in spatially interconnected structures, 2018, Pages 2653:2658. European Control Conference (ECC).
- M.H. Abbasi, L. Iapichino, S. Naderilordejani, W.H.A. Schilders, N. van de Wouw, Reduced basis method for hyperbolic systems with nonlinear boundary conditions, 2018, 6th European Conference on Computational Mechanics, 7th European Conference on Computational Fluid Dynamics (ECFD 7).
- S. Naderilordejani, B. Besselink, M.H. Abbasi, G.O. Kaasa, W.H.A. Schilders, and N. van de Wouw, Control-oriented modeling and model order reduction for managed pressure drilling systems, 2018, 4th International Colloquium on Non-linear dynamics and control of deep drilling systems. U.J.F. Aarsnes, E. Detournay, N. van de Wouw, and V. Denoël (eds.). San Francisco: IRIS, p. 109-120
2017
Journal Publications:
-
B.A. de Dios, R. Hiptmair, and C. Pagliantini, Auxiliary space preconditioners for SIP-DG discretizations of H(curl)-elliptic problems with discontinuous coefficients, IMA J. Numer. Anal., 37(2) (2017), pp. 646-686.
- L. Iapichino, S. Ulbrich and S. Volkwein. Multi-objective pde-constrained optimization using the reduced basis method. Advances in Computational Mathematics, (2017) 1-28.
- S. Korzilius, W.H.A. Schilders, and M.J.H. Anthonissen, An Improved CSPM Approach for Accurate Second-Derivative Approximations with SPH, 25 Jan 2017, In : Journal of Applied Mathematics and Physics. 5, 1, p. 168-184 17 p.
- G. De Luca, P. Bolcato, R. Larcheveque, J. Rommes, and W.H.A. Schilders, Fast and accurate time-domain simulations of integer-N PLLs, 1 Apr 2017, In : IEEE Transactions on Circuits and Systems I: Regular Papers. 64, 4, p. 931-944 14 p., 7792570.
- S.P. Korzilius, A.S. Tijsseling, Z. Bozkus, M.J.H. Anthonissen, and W.H.A. Schilders, Modeling liquid slugs accelerating in inclined conduits 1 Dec 2017, In : Journal of Pressure Vessel Technology. Transactions of the ASME. 139, 6, 10 p., 061301.
Conference Publications:
- S. Lungten, R. Bornoff, J. Dyson, J.M.L. Maubach, W.H.A. Schilders, and M. Warner, Dynamic compact thermal model extraction for LED packages using model order reduction techniques, Sep 2017, THERMINIC 2017 – 23rd International Workshop on Thermal Investigations of ICs and Systems. Piscataway: Institute of Electrical and Electronics Engineers, Vol. 2017-January. p. 1-6 6 p.
- A.K. Tyagi, X. Jonsson, T.G.J. Beelen, and W.H.A. Schilders, Speeding up rare event simulations using Kriging models, 7 Jun 2017, 2017 IEEE 21st Workshop on Signal and Power Integrity, SPI 2017 – Proceedings. Piscataway: Institute of Electrical and Electronics Engineers, 4 p. 7944001
2016
Journal Publications:
- H. Heumann, R. Hiptmair, and C. Pagliantini, Stabilized Galerkin for transient advection of differential forms, Discrete Contin. Dyn. Syst. Ser. S, 9.1 (2016), pp. 185-214.
- L. Iapichino, S. Volkwein and A. Wesche. A-posteriori error analysis for lithium-ion concentrations in batteries utilizing the reduced basis method. Mathematical and Computer Modelling of Dynamical Systems: Methods, Tools and Applications in Engineering and Related Sciences, (2016) 22: 362-379.
- L. Iapichino, A. Quarteroni, and G. Rozza. Reduced basis method and domain decomposition for elliptic problems in networks and complex parametrized geometries. Computers & Mathematics with Applications, (2016) 71(1):408-430.
- S. Lungten, W.H.A. Schilders, and J.M.L. Maubach, Sparse block factorization of saddle point matrices, 2016, In : Linear Algebra and Its Applications. 502, p. 214–242 29 p.
Conference Publications:
- R.J. Dedden, L. Iapichino, Paolo Tiso, J.F.L. Goosen, F. van Keulen. Efficient residual stress identification approach for MEMS using modal information. Proceedings of Isma2016 International Conference on Noise and Vibration Engineering and Usd2016 International Conference on Uncertainty in Structural Dynamics, p.2169-2181, 2016.
- L. Iapichino, S.Trenz and S. Volkwein. Reduced-order multiobjective optimal control of semilinear parabolic problems. Numerical Mathematics and Advanced Applications ENUMATH 2015, p. 389-397, 2016.
- G. De Luca, W.H.A. Schilders, P. Bolcato, R. Larcheveque, and J. Rommes, Accelerating time domain simulations of PLLs, 20 Jun 2016, 2016 IEEE 20th Workshop on Signal and Power Integrity, SPI 2016 – Proceedings. Institute of Electrical and Electronics Engineers, 4 p. 7496299
- R. Bornoff, V. Hildenbrand, S. Lungten, G. Martin, C. Marty, A. Poppe, M. Rencz, W.H.A. Schilders, and J. Yu, Delphi4LED – From measurements to standardized multi-domain compact models of LED: A new European R&D project for predictive and efficient multi-domain modeling and simulation of LEDs at all integration levels along the SSL supply chain, 18 Nov 2016, THERMINIC 2016 – 22nd International Workshop on Thermal Investigations of ICs and Systems. Institute of Electrical and Electronics Engineers, p. 174-180 7 p. 7749048
